Skinnerův chlívek

JIRKA:
Velmi mě zaujal váš výklad o tom, jak se mění strategie hráčů, když neuvažují v rámci jedné partie, ale celé dlouhé, případně nekonečné, série stejných partií. Uvědomil jsem si, že asi tak nějak probíhala přírodní evoluce, Darwinův vývoj druhů.

JEFF:
Děláte mi radost. Je to tak. Dnes se to shrnuje do oblasti Evoluční teorie her. Klasické pojetí teorie her vychází při aplikaci kooperativních i nekooperativních her ze dvou předpokladu. Za prvé, že hráči jsou neomezeně racionální, a za druhé, že se rozhodují s plnou informací o situaci a úmyslech protihráče. Jenže v praxi to nebývá splněno. Proto i získané výsledky nejsou vždy bez výhrad přenositelné do reálu.

JIRKA:
Takže, když se hra znovu a znovu opakuje, hráči se učí volit svou optimální strategii, aby dlouhodobě získali, co největší užitek. Hledá se stabilita systému.

JEFF:
Přesně tak. Velice názorný je experiment, který v roce 1979 provedli B. A. Baldwin a G. B. Meese. Je znám pod názvem Skinnerův chlívek.
Představte si trochu větší chlívek. Na jednom konci chlívku je páka, za kterou, když se zatáhne, se na druhém konci chlívku z nálevky nasype krmení do koryta.

JIRKA:
Prase se naučilo, že stisknutí páky nasype do koryta potravu? Tak teď tráví čas pobíháním mezi korytem a pákou.

JEFF:
To se stalo, když do chlívku dali jedno práce. Ale oni šli dál. Do chlívku zavřeli prasata dvě. Jedno velké dominantní a druhé malé submisivní. Tak vytvořili možnost, aby jedno prase vykořisťovalo druhé. Jak odhadujete, co se bude ve chlívku dít?

JIRKA:
Viděl jsem mnohokrát, jak se chovají prasata u koryta, kdy každé odstrkuje každé. Takže to velké bude stát u koryta a malé tahat za páku a pak se snažit aspoň trochu vecpat k žrádlu.

JEFF:
Totéž očekávali zmínění páni. Nicméně nastalo následující. Popíšeme si to jako příběh o deseti obrazech. Zapojte svou představivost.

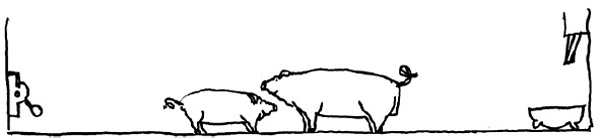
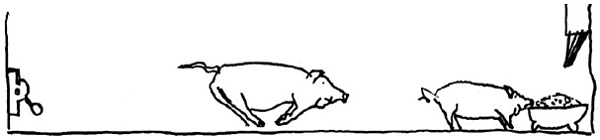
1. obraz – prasata na sebe čumí uprostřed chlívku	2. obraz – malé zkoumá páku a zatáhne ji; do koryta se nasype potrava a velké běží ke korytu
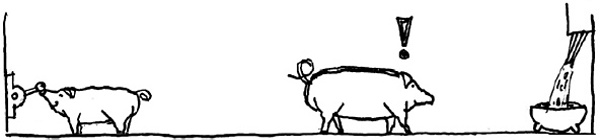
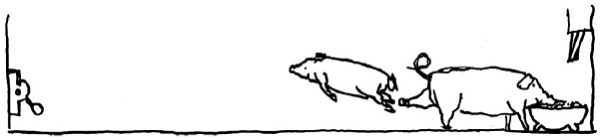
3. obraz – velké se cpe a malé se běží také přiživit	4. obraz – velké nepustí malé ke korytu, odkopne ho
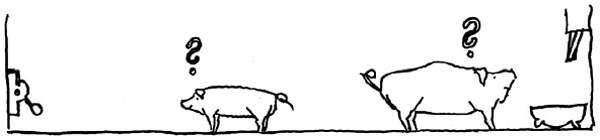
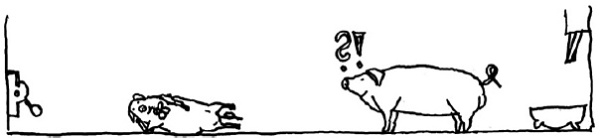
5. obraz – potrava došla, velké se diví a čeká další dávku, malé přemýšlí, co teď	6. obraz – malé simuluje neschopnost
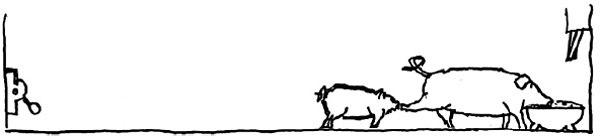
7. obraz – velké pochopí, že musí stisknout páku, za jeho zády malé přejde ke korytu	8. obraz – velké běží ke korytu, u kterého se malé cpe
9. obraz – velké odstrkuje malé a cpe se samo	10. obraz – potrava došla, malé simuluje neschopnost

A tak se to opakuje. Nakonec malé čeká u koryta, velké stiskne páku, než velké přeběhne chlívek, nažere se malé, které je následně odehnáno, a velké vše dožere. Atd.

Ukazuje se, že strategie: jsi-li dominantní, seď u koryta, jsi-li submisivní, mačkej páku, vypadá na první pohled rozumně, není však rovnovážná: submisivní prase by běhalo od páky ke korytu, a nikdy by za svou námahu nebylo odměněno, protože dominantní prase by je k potravě nepustilo. Výhodnější pro něj je nedělat nic, protože aspoň neztrácí energii. Brzy proto s touto zbytečnou snahou skončí a dominantnímu praseti nezbude, než mačkat páku samo. Nakonec tedy bude submisivní prase čekat u koryta a velké bude mačkat páku a pak se vždy vyřítí přes celý chlívek ke korytu, odstrčí submisivní prase, které zatím stačilo aspoň něco pojíst, a dojí zbytek.

Pokus skutečně takto dopadl, a to dokonce i v případě, že dávka potravy byla tak malá, že submisivní prase stačilo sníst více potravy než dominantní. Dvojice strategií (mačkej páku, seď u koryta) je rovnovážným bodem.

JIRKA:
Z toho plyne poučení, že dominantní musí mačkat páku, aby se najedli, zatímco submisivní sedí pohodlně u koryta a jen čekají, co se jim nasype. Díky Skinnerovu chlívku aspoň víme, že je to daň za stabilitu.

JEFF:
Jak to bude vypadat čistě matematicky, ukazuje dvojmatice:

V modelu jsme uvažovali zisk z celé dávky potravy v hodnotě 10 jednotek užitku, ztrátu danou námahou spojenou s mačkáním páky a běháním v hodnotě −2 jednotek a množství potravy, které submisivní prase stačí pojíst, než je odstrčeno dominantním, v hodnotě 4 jednotek.
Racionálně uvažující hráči by dospěli k rovnovážným strategiím následujícím způsobem. Z pohledu submisivního hráče je první strategie dominována druhou a může být proto rovnou eliminována. Dominantní hráč předpokládá racionalitu svého protivníka a uvědomí si, že bude volit svou druhou strategii; rozhoduje se tedy mezi ziskem 0 a 6 jednotek, což jej dovede k volbě první strategie. Postupným eliminováním dominovaných strategií tak racionální rozhodovatelé došli ke stejnému závěru jako naše pokusná zvířata – ke dvojici rovnovážných strategií (mačkej páku, seď u koryta). Snadno se nahlédne, že tato dvojice strategií splňuje podmínku pro rovnovážné strategie.

JIRKA:
Ta čísla v dvojmatici jsou náhodná, nebo mají hlubší smysl?

JEFF:
Hodnoty jsem zvolil náhodně a je možné je libovolně změnit. Ze strategického hlediska se nic nezmění, ohodnotíme-li námahu libovolným záporným číslem, získá-li čekající submisivní prase nezáporný počet jednotek a nezáporný počet jednotek zbude na prase dominantní. Výsledek bude stejný.
Brzy se ukázalo nejen to, že principy chování živočichů i rostlin při vzájemných interakcích i celou evoluční teorii lze zatím nejuspokojivěji objasnit z pohledu teorie her, ale dokonce i to, že nejslibnější aplikace teorie her jsou právě v biologii.

JIRKA:
To, co zde říkáte, je úžasné. Dovedu pochopit, že problematika konfliktu či spolupráce různých živých organismů do teorie her svým obsahem patří. Na druhé straně si těžko představím, že třeba sršeň nebo jabloňový list si sestaví matematický model, vytvoří si přehled svých strategií, ocení možné výstupy a určí optimální strategii.

JEFF:
Ukazuje se, že dokonce čím méně je vyvinutá schopnost organismu přemýšlet, tím lépe pro něj teorie her funguje.

JIRKA:
Takže je lepší nemyslet? No, mnozí lidé si to myslí.